ichol
Incomplete Cholesky factorization
Description
L = ichol(A)A with zero-fill.
A must be a sparse square matrix.
Examples
Incomplete Cholesky Factorization
This example generates an incomplete Cholesky factorization.
Start with a symmetric positive definite matrix, A:
N = 100;
A = delsq(numgrid('S',N));A is the two-dimensional, five-point discrete negative Laplacian on a 100-by-100 square grid with Dirichlet boundary conditions. The size of A is 98*98 = 9604 (not 10000 as the borders of the grid are used to impose the Dirichlet conditions).
The no-fill incomplete Cholesky factorization is a factorization which contains only nonzeros in the same position as A contains nonzeros. This factorization is extremely cheap to compute. Although the product L*L' is typically very different from A, the product L*L' will match A on its pattern up to round-off.
L = ichol(A); norm(A-L*L','fro')./norm(A,'fro')
ans = 0.0916
norm(A-(L*L').*spones(A),'fro')./norm(A,'fro')
ans = 4.9606e-17
ichol may also be used to generate incomplete Cholesky factorizations with threshold dropping. As the drop tolerance decreases, the factor tends to get more dense and the product L*L' tends to be a better approximation of A. The following plots show the relative error of the incomplete factorization plotted against the drop tolerance as well as the ratio of the density of the incomplete factors to the density of the complete Cholesky factor.
n = size(A,1); ntols = 20; droptol = logspace(-8,0,ntols); nrm = zeros(1,ntols); nz = zeros(1,ntols); nzComplete = nnz(chol(A,'lower')); for k = 1:ntols L = ichol(A,struct('type','ict','droptol',droptol(k))); nz(k) = nnz(L); nrm(k) = norm(A-L*L','fro')./norm(A,'fro'); end figure loglog(droptol,nrm,'LineWidth',2) title('Drop tolerance vs norm(A-L*L'',''fro'')./norm(A,''fro'')')
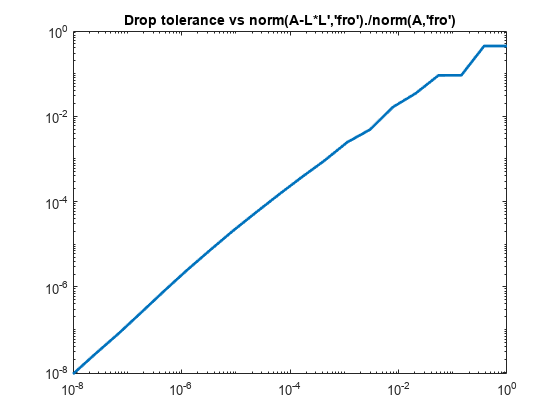
figure semilogx(droptol,nz./nzComplete,'LineWidth',2) title('Drop tolerance vs fill ratio ichol/chol')
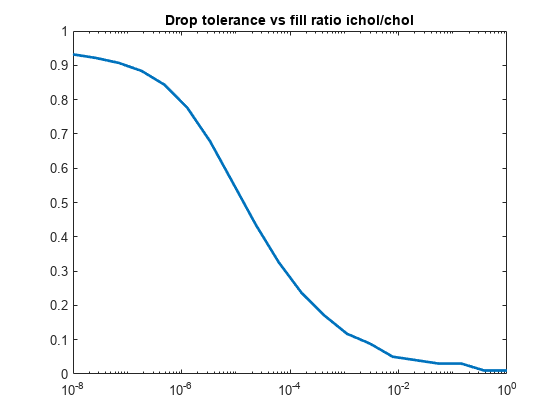
The relative error is typically on the same order as the drop tolerance, although this is not guaranteed.
Using ichol as a Preconditioner
This example shows how to use an incomplete Cholesky factorization as a preconditioner to improve convergence.
Create a symmetric positive definite matrix, A.
N = 100;
A = delsq(numgrid('S',N));Create an incomplete Cholesky factorization as a preconditioner for pcg. Use a constant vector as the right hand side. As a baseline, execute pcg without a preconditioner.
b = ones(size(A,1),1); tol = 1e-6; maxit = 100; [x0,fl0,rr0,it0,rv0] = pcg(A,b,tol,maxit);
Note that fl0 = 1 indicating that pcg did not drive the relative residual to the requested tolerance in the maximum allowed iterations. Try the no-fill incomplete Cholesky factorization as a preconditioner.
L1 = ichol(A); [x1,fl1,rr1,it1,rv1] = pcg(A,b,tol,maxit,L1,L1');
fl1 = 0, indicating that pcg converged to the requested tolerance and did so in 59 iterations (the value of it1). Since this matrix is a discretized Laplacian, however, using modified incomplete Cholesky can create a better preconditioner. A modified incomplete Cholesky factorization constructs an approximate factorization that preserves the action of the operator on the constant vector. That is, norm(A*e-L*(L'*e)) will be approximately zero for e = ones(size(A,2),1) even though norm(A-L*L','fro')/norm(A,'fro') is not close to zero. It is not necessary to specify type for this syntax since nofill is the default, but it is good practice.
options.type = 'nofill'; options.michol = 'on'; L2 = ichol(A,options); e = ones(size(A,2),1); norm(A*e-L2*(L2'*e))
ans = 3.7983e-14
[x2,fl2,rr2,it2,rv2] = pcg(A,b,tol,maxit,L2,L2');
pcg converges (fl2 = 0) but in only 38 iterations. Plotting all three convergence histories shows the convergence.
semilogy(0:maxit,rv0./norm(b),'b.'); hold on semilogy(0:it1,rv1./norm(b),'r.'); semilogy(0:it2,rv2./norm(b),'k.'); legend('No Preconditioner','IC(0)','MIC(0)');
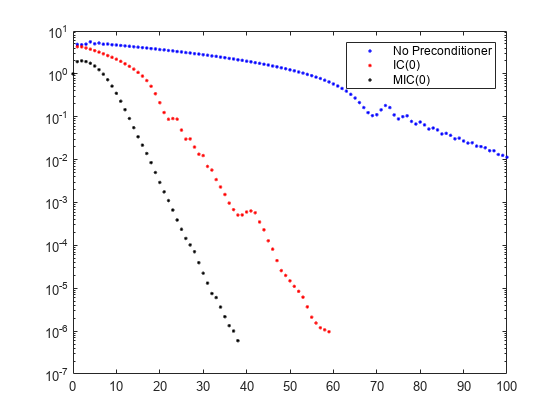
The plot shows that the modified incomplete Cholesky preconditioner creates a much faster convergence.
You can also try incomplete Cholesky factorizations with threshold dropping. The following plot shows convergence of pcg with preconditioners constructed with various drop tolerances.
L3 = ichol(A, struct('type','ict','droptol',1e-1)); [x3,fl3,rr3,it3,rv3] = pcg(A,b,tol,maxit,L3,L3'); L4 = ichol(A, struct('type','ict','droptol',1e-2)); [x4,fl4,rr4,it4,rv4] = pcg(A,b,tol,maxit,L4,L4'); L5 = ichol(A, struct('type','ict','droptol',1e-3)); [x5,fl5,rr5,it5,rv5] = pcg(A,b,tol,maxit,L5,L5'); figure semilogy(0:maxit,rv0./norm(b),'b-','linewidth',2); hold on semilogy(0:it3,rv3./norm(b),'b-.','linewidth',2); semilogy(0:it4,rv4./norm(b),'b--','linewidth',2); semilogy(0:it5,rv5./norm(b),'b:','linewidth',2); legend('No Preconditioner','ICT(1e-1)','ICT(1e-2)', ... 'ICT(1e-3)','Location','SouthEast');
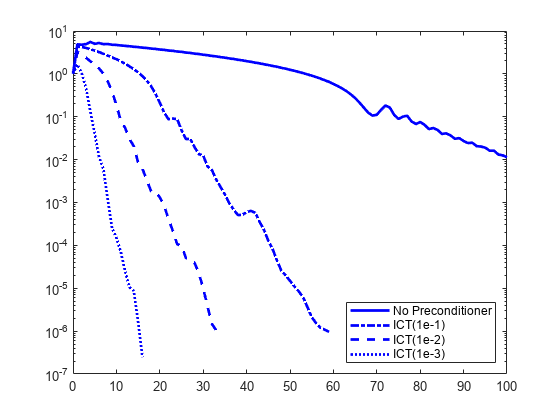
Note the incomplete Cholesky preconditioner constructed with drop tolerance 1e-2 is denoted as ICT(1e-2).
As with the zero-fill incomplete Cholesky, the threshold dropping factorization can benefit from modification (i.e. options.michol = 'on') since the matrix arises from an elliptic partial differential equation. As with MIC(0), the modified threshold based dropping incomplete Cholesky will preserve the action of the preconditioner on constant vectors, that is norm(A*e-L*(L'*e)) will be approximately zero.
Using the diagcomp Option
This example illustrates the use of the diagcomp option of ichol.
Incomplete Cholesky factorizations of positive definite matrices do not always exist. The following code constructs a random symmetric positive definite matrix and attempts to solve a linear system using pcg.
S = rng('default');
A = sprandsym(1000,1e-2,1e-4,1);
rng(S);
b = full(sum(A,2));
[x0,fl0,rr0,it0,rv0] = pcg(A,b,1e-6,100);Since convergence is not attained, try to construct an incomplete Cholesky preconditioner.
L = ichol(A,struct('type','ict','droptol',1e-3));
Error using ichol Encountered nonpositive pivot.
If ichol breaks down as above, you can use the diagcomp option to construct a shifted incomplete Cholesky factorization. That is, instead of constructing L such that L*L' approximates A, ichol with diagonal compensation constructs L such that L*L' approximates M = A + alpha*diag(diag(A)) without explicitly forming M. As incomplete factorizations always exist for diagonally dominant matrices, alpha can be found to make M diagonally dominant.
alpha = max(sum(abs(A),2)./diag(A))-2
alpha = 62.9341
L1 = ichol(A, struct('type','ict','droptol',1e-3,'diagcomp',alpha)); [x1,fl1,rr1,it1,rv1] = pcg(A,b,1e-6,100,L1,L1');
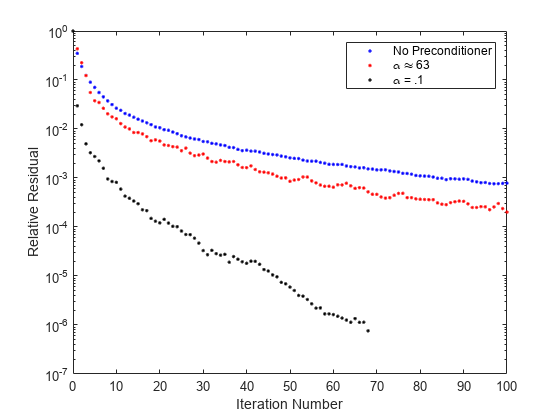
Here, pcg still fails to converge to the desired tolerance within the desired number of iterations, but as the plot below shows, convergence is better for pcg with this preconditioner than with no preconditioner. Choosing a smaller alpha may help. With some experimentation, we can settle on an appropriate value for alpha.
alpha = .1; L2 = ichol(A, struct('type','ict','droptol',1e-3,'diagcomp',alpha)); [x2,fl2,rr2,it2,rv2] = pcg(A,b,1e-6,100,L2,L2');
Now, pcg converges and a plot can show the convergence histories with each preconditioner.
semilogy(0:100,rv0./norm(b),'b.'); hold on; semilogy(0:100,rv1./norm(b),'r.'); semilogy(0:it2,rv2./norm(b),'k.'); legend('No Preconditioner','\alpha \approx 63','\alpha = .1'); xlabel('Iteration Number'); ylabel('Relative Residual');
Input Arguments
A — Input matrix
sparse square matrix
Input matrix, specified as a sparse square matrix.
options — Cholesky factorization options
structure
Cholesky factorization options, specified as a structure with up to five fields:
| Field Name | Summary | Description |
|---|---|---|
type | Type of factorization | Indicates which flavor of incomplete Cholesky to perform. Valid
values of this field are |
droptol | Drop tolerance when type is 'ict' | Nonnegative scalar used as a drop tolerance when performing ICT.
Elements which are smaller in magnitude than a local drop tolerance are
dropped from the resulting factor except for the diagonal element which is
never dropped. The local drop tolerance at step |
michol | Indicates whether to perform modified incomplete Cholesky | Indicates whether or not modified incomplete
Cholesky (MIC) is performed. The field may be
|
diagcomp | Perform compensated incomplete Cholesky with the specified coefficient | Real nonnegative scalar used as a global diagonal shift
|
shape | Determines which triangle is referenced and returned | Valid values are |
Example: options.type = 'nofill'; options.michol = 'on'; L =
ichol(A,options);
Tips
References
[1] Saad, Yousef. “Preconditioning Techniques.” Iterative Methods for Sparse Linear Systems. PWS Publishing Company, 1996.
[2] Manteuffel, T.A. “An incomplete factorization technique for positive definite linear systems.” Math. Comput. 34, 473–497, 1980.
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
Usage notes and limitations:
If you specify the
typefield ofoptions, it must be'nofill'.Amust be real symmetric or complex hermitian.
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced in R2011a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)