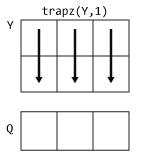
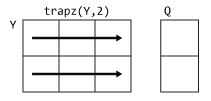
trapz
Trapezoidal numerical integration
Description
Q = trapz( computes the approximate integral of
Y)Y via the trapezoidal method with unit spacing. The size of
Y determines the dimension to integrate along:
If
Yis a vector, thentrapz(Y)is the approximate integral ofY.If
Yis a matrix, thentrapz(Y)integrates over each column and returns a row vector of integration values.If
Yis a multidimensional array, thentrapz(Y)integrates over the first dimension whose size does not equal 1. The size of this dimension becomes 1, and the sizes of other dimensions remain unchanged.
Q = trapz(___, integrates along the
dimension dim)dim using any of the previous syntaxes. You must
specify Y, and optionally can specify X.
If you specify X, then it can be a scalar or a vector with
length equal to size(Y,dim). For example, if
Y is a matrix, then trapz(X,Y,2)
integrates each row of Y.
Examples
Input Arguments
More About
Tips
Use
trapzandcumtrapzto perform numerical integrations on discrete data sets. Useintegral,integral2, orintegral3instead if a functional expression for the data is available.trapzreduces the size of the dimension it operates on to 1, and returns only the final integration value.cumtrapzalso returns the intermediate integration values, preserving the size of the dimension it operates on.
Extended Capabilities
Version History
Introduced before R2006a