Unconstrained Nonlinear Optimization Algorithms
Unconstrained Optimization Definition
Unconstrained minimization is the problem of finding a vector x that is a local minimum to a scalar function f(x):
The term unconstrained means that no restriction is placed on the range of x.
fminunc trust-region Algorithm
Trust-Region Methods for Nonlinear Minimization
Many of the methods used in Optimization Toolbox™ solvers are based on trust regions, a simple yet powerful concept in optimization.
To understand the trust-region approach to optimization, consider the unconstrained minimization problem, minimize f(x), where the function takes vector arguments and returns scalars. Suppose you are at a point x in n-space and you want to improve, i.e., move to a point with a lower function value. The basic idea is to approximate f with a simpler function q, which reasonably reflects the behavior of function f in a neighborhood N around the point x. This neighborhood is the trust region. A trial step s is computed by minimizing (or approximately minimizing) over N. This is the trust-region subproblem,
| (1) |
The current point is updated to be x + s if f(x + s) < f(x); otherwise, the current point remains unchanged and N, the region of trust, is shrunk and the trial step computation is repeated.
The key questions in defining a specific trust-region approach to minimizing f(x) are how to choose and compute the approximation q (defined at the current point x), how to choose and modify the trust region N, and how accurately to solve the trust-region subproblem. This section focuses on the unconstrained problem. Later sections discuss additional complications due to the presence of constraints on the variables.
In the standard trust-region method ([48]), the quadratic approximation q is defined by the first two terms of the Taylor approximation to F at x; the neighborhood N is usually spherical or ellipsoidal in shape. Mathematically the trust-region subproblem is typically stated
| (2) |
where g is the gradient of f at the current point x, H is the Hessian matrix (the symmetric matrix of second derivatives), D is a diagonal scaling matrix, Δ is a positive scalar, and ‖ . ‖ is the 2-norm. Good algorithms exist for solving Equation 2 (see [48]); such algorithms typically involve the computation of all eigenvalues of H and a Newton process applied to the secular equation
Such algorithms provide an accurate solution to Equation 2. However, they require time proportional to several factorizations of H. Therefore, for large-scale problems a different approach is needed. Several approximation and heuristic strategies, based on Equation 2, have been proposed in the literature ([42] and [50]). The approximation approach followed in Optimization Toolbox solvers is to restrict the trust-region subproblem to a two-dimensional subspace S ([39] and [42]). Once the subspace S has been computed, the work to solve Equation 2 is trivial even if full eigenvalue/eigenvector information is needed (since in the subspace, the problem is only two-dimensional). The dominant work has now shifted to the determination of the subspace.
The two-dimensional subspace S is determined with the aid of a preconditioned conjugate gradient process described below. The solver defines S as the linear space spanned by s1 and s2, where s1 is in the direction of the gradient g, and s2 is either an approximate Newton direction, i.e., a solution to
| (3) |
or a direction of negative curvature,
| (4) |
The philosophy behind this choice of S is to force global convergence (via the steepest descent direction or negative curvature direction) and achieve fast local convergence (via the Newton step, when it exists).
A sketch of unconstrained minimization using trust-region ideas is now easy to give:
Formulate the two-dimensional trust-region subproblem.
Solve Equation 2 to determine the trial step s.
If f(x + s) < f(x), then x = x + s.
Adjust Δ.
These four steps are repeated until convergence. The trust-region dimension Δ is adjusted according to standard rules. In particular, it is decreased if the trial step is not accepted, i.e., f(x + s) ≥ f(x). See [46] and [49] for a discussion of this aspect.
Optimization Toolbox solvers treat a few important special cases of f with specialized functions: nonlinear least-squares, quadratic functions, and linear least-squares. However, the underlying algorithmic ideas are the same as for the general case. These special cases are discussed in later sections.
Preconditioned Conjugate Gradient Method
A popular way to solve large, symmetric, positive definite systems of linear equations Hp = –g is the method of Preconditioned Conjugate Gradients (PCG). This iterative approach requires the ability to calculate matrix-vector products of the form H·v where v is an arbitrary vector. The symmetric positive definite matrix M is a preconditioner for H. That is, M = C2, where C–1HC–1 is a well-conditioned matrix or a matrix with clustered eigenvalues.
In a minimization context, you can assume that the Hessian matrix H is symmetric. However, H is guaranteed to be positive definite only in the neighborhood of a strong minimizer. Algorithm PCG exits when it encounters a direction of negative (or zero) curvature, that is, dTHd ≤ 0. The PCG output direction p is either a direction of negative curvature or an approximate solution to the Newton system Hp = –g. In either case, p helps to define the two-dimensional subspace used in the trust-region approach discussed in Trust-Region Methods for Nonlinear Minimization.
fminunc quasi-newton Algorithm
Basics of Unconstrained Optimization
Although a wide spectrum of methods exists for unconstrained optimization, methods can be broadly categorized in terms of the derivative information that is, or is not, used. Search methods that use only function evaluations (e.g., the simplex search of Nelder and Mead [30]) are most suitable for problems that are not smooth or have a number of discontinuities. Gradient methods are generally more efficient when the function to be minimized is continuous in its first derivative. Higher order methods, such as Newton's method, are only really suitable when the second-order information is readily and easily calculated, because calculation of second-order information, using numerical differentiation, is computationally expensive.
Gradient methods use information about the slope of the function to dictate a direction of search where the minimum is thought to lie. The simplest of these is the method of steepest descent in which a search is performed in a direction, –∇f(x), where ∇f(x) is the gradient of the objective function. This method is very inefficient when the function to be minimized has long narrow valleys as, for example, is the case for Rosenbrock's function
| (5) |
The minimum of this function is at x = [1,1], where f(x) = 0. A contour map of this function is shown in the figure below, along with the solution path to the minimum for a steepest descent implementation starting at the point [–2,2]. The optimization was terminated after 400 iterations, still a considerable distance from the minimum. The black areas are where the method is continually zigzagging from one side of the valley to another.
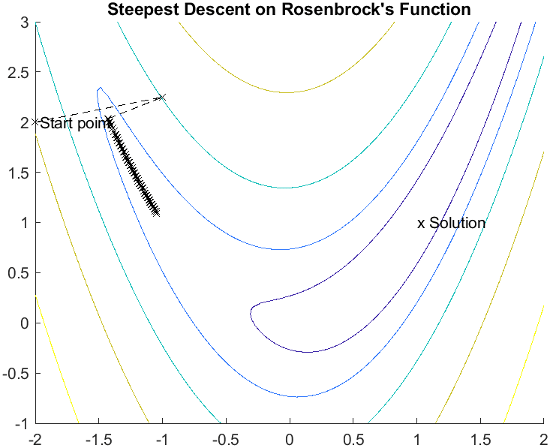
This function, also known as the banana function, is notorious in unconstrained examples because of the way the curvature bends around the origin. Rosenbrock's function is used throughout this section to illustrate the use of a variety of optimization techniques. The contours have been plotted in exponential increments because of the steepness of the slope surrounding the U-shaped valley.
For a more complete description of this figure, including scripts that generate the iterative points, see Banana Function Minimization.
Quasi-Newton Methods
Of the methods that use gradient information, the most favored are the quasi-Newton methods. These methods build up curvature information at each iteration to formulate a quadratic model problem of the form
| (6) |
where the Hessian matrix, H, is a positive definite symmetric matrix, c is a constant vector, and b is a constant. The optimal solution for this problem occurs when the partial derivatives of x go to zero, i.e.,
| (7) |
The optimal solution point, x*, can be written as
| (8) |
Newton-type methods (as opposed to quasi-Newton methods) calculate H directly and proceed in a direction of descent to locate the minimum after a number of iterations. Calculating H numerically involves a large amount of computation. Quasi-Newton methods avoid this by using the observed behavior of f(x) and ∇f(x) to build up curvature information to make an approximation to H using an appropriate updating technique.
A large number of Hessian updating methods have been developed. However, the formula of Broyden [3], Fletcher [12], Goldfarb [20], and Shanno [37] (BFGS) is thought to be the most effective for use in a general purpose method.
The formula given by BFGS is
| (9) |
where
As a starting point, H0 can be set to any symmetric positive definite matrix, for example, the identity matrix I. To avoid the inversion of the Hessian H, you can derive an updating method that avoids the direct inversion of H by using a formula that makes an approximation of the inverse Hessian H–1 at each update. A well-known procedure is the DFP formula of Davidon [7], Fletcher, and Powell [14]. This uses the same formula as the BFGS method (Equation 9) except that qk is substituted for sk.
The gradient information is either supplied through analytically calculated gradients, or derived by partial derivatives using a numerical differentiation method via finite differences. This involves perturbing each of the design variables, x, in turn and calculating the rate of change in the objective function.
At each major iteration, k, a line search is performed in the direction
| (10) |
The quasi-Newton method is illustrated by the solution path on Rosenbrock's function. The method is able to follow the shape of the valley and converges to the minimum after about 150 function evaluations using only finite difference gradients.
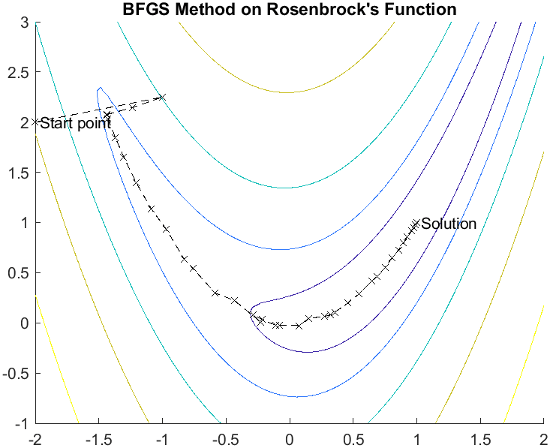
For a more complete description of this figure, including scripts that generate the iterative points, see Banana Function Minimization.
Line Search
Line search is a search method that is used as part of a larger optimization algorithm. At each step of the main algorithm, the line-search method searches along the line containing the current point, xk, parallel to the search direction, which is a vector determined by the main algorithm. That is, the method finds the next iterate xk+1 of the form
| (11) |
where xk denotes the current iterate, dk is the search direction, and α* is a scalar step length parameter.
The line search method attempts to decrease the objective function along the line xk + α*dk by repeatedly minimizing polynomial interpolation models of the objective function. The line search procedure has two main steps:
The bracketing phase determines the range of points on the line to be searched. The bracket corresponds to an interval specifying the range of values of α.
The sectioning step divides the bracket into subintervals, on which the minimum of the objective function is approximated by polynomial interpolation.
The resulting step length α satisfies the Wolfe conditions:
| (12) |
| (13) |
where c1 and c2 are constants with 0 < c1 < c2 < 1.
The first condition (Equation 12) requires that αk sufficiently decreases the objective function. The second condition (Equation 13) ensures that the step length is not too small. Points that satisfy both conditions (Equation 12 and Equation 13) are called acceptable points.
The line search method is an implementation of the algorithm described in Section 2-6 of [13]. See also [31] for more information about line search.
Hessian Update
Many of the optimization functions determine the direction of search by
updating the Hessian matrix at each iteration, using the BFGS method (Equation 9).
The function fminunc also provides an option to
use the DFP method given in Quasi-Newton Methods (set HessUpdate to
'dfp' in options to select the DFP
method). The Hessian, H, is always maintained to be positive
definite so that the direction of search, d, is always in a
descent direction. This means that for some arbitrarily small step
α in the direction d, the objective
function decreases in magnitude. You achieve positive definiteness of
H by ensuring that H is initialized to
be positive definite and thereafter (from Equation 14) is always positive. The term is a product of the line search step length parameter
αk and a combination of the
search direction d with past and present gradient
evaluations,
| (14) |
You always achieve the condition that is positive by performing a sufficiently accurate line search. This is because the search direction, d, is a descent direction, so that αk and the negative gradient –∇f(xk)Td are always positive. Thus, the possible negative term –∇f(xk+1)Td can be made as small in magnitude as required by increasing the accuracy of the line search.
LBFGS Hessian Approximation
For large problems, the BFGS Hessian approximation method can be relatively
slow and use a large amount of memory. To circumvent these issues, use the LBFGS
Hessian approximation by setting the HessianApproximation
option to 'lbfgs'. This causes fminunc
to use the Low-memory BFGS Hessian approximation, described next. For the
benefit of using LBFGS in a large problem, see Solve Nonlinear Problem with Many Variables.
As described in Nocedal and Wright [31], the Low-memory BFGS Hessian approximation is similar to the BFGS approximation described in Quasi-Newton Methods, but uses a limited amount of memory for previous iterations. The Hessian update formula given in Equation 9 is
where
Another description of the BFGS procedure is
| (15) |
where ɑk is the step length chosen by line search, and Hk is an inverse Hessian approximation. The formula for Hk:
where sk and qk are defined as before, and
For the LBFGS algorithm, the algorithm keeps a fixed, finite number m of the parameters sk and qk from the immediately preceding iterations. Starting from an initial H0, the algorithm computes an approximate Hk for obtaining the step from Equation 15. The computation of proceeds as a recursion from the preceding equations using the most recent m values of ρj, qj, and sj. For details, see Algorithm 7.4 of Nocedal and Wright [31].

