Ravigneaux Gear
Planetary gear with two sun gears and two planet gear sets
Libraries:
Simscape /
Driveline /
Gears
Description
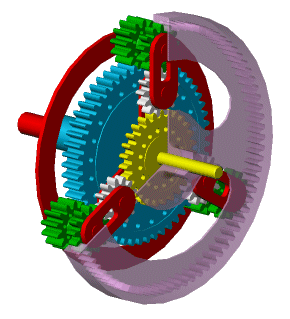
The Ravigneaux Gear block represents a planetary gear train with dual sun and planet gear sets. The two sun gears are centrally located and separated longitudinally along a common rotation axis. The smaller of these gears engages an inner planet gear set, which in turn engages an outer planet gear set. The outer planet gear set, whose length spans the distance between the two sun gears, engages both the larger sun gear and the ring gear.
A carrier holds the planet gear sets in place at different radii. The carrier, which rigidly connects to a drive shaft, can spin as a unit with respect to the sun and ring gears. Revolute joints, each located between a planet gear and the carrier, enable the gears to spin about their individual longitudinal axes.
The relative angular velocities of the sun, planet, and ring gears follow from the kinematic constraints between them. For more information, see Equations.
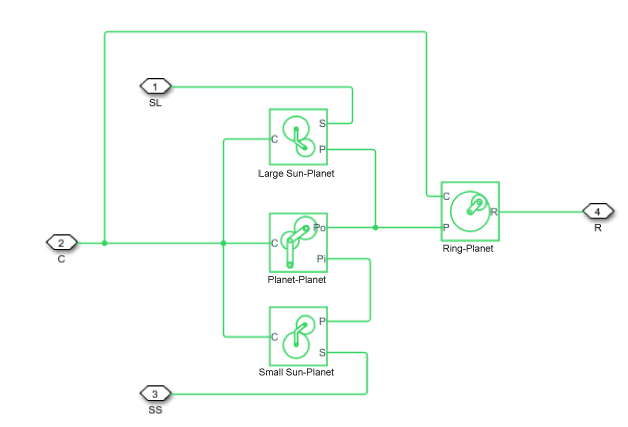
The block models the Ravigneaux gear as a structural component based on the Sun-Planet, Planet-Planet, and Ring-Planet Simscape™ Driveline™ blocks. The figure shows the equivalent block diagram of this structural component.
To increase the fidelity of the gear model, you can specify properties such as gear inertia, meshing losses, and viscous losses. By default, gear inertia and viscous losses are assumed to be negligible. The block enables you to specify the inertias of the internal planet gears. To model the inertias of the carrier, large sun, small sun, and ring gears, connect Simscape Inertia blocks to ports C, SL, SS, and R.
Thermal Model
You can model
the effects of heat flow and temperature change by enabling the optional thermal port. To enable
the port, set Friction model to Temperature-dependent
efficiency.
Equations
The Ravigneaux Gear block imposes four kinematic and four geometric constraints on the four connected axes and the two internal wheels (the inner and outer planet gears):
where:
rCi is the radius of the inner carrier gear.
ωC is the angular velocity of the carrier gears.
rSS is the radius of the small sun gear.
ωSS is the angular velocity of the small sun gear.
rPi is the radius of the inner planet gear.
ωPi is the angular velocity of the inner planet gear.
rCo is the radius of the outer carrier gear.
rSL is the radius of the large sun gear.
ωSL is the angular velocity of the large sun gear.
rPo is the radius of the outer planet gear.
ωPo is the angular velocity of the outer planet gear.
ωR is the angular velocity of the ring gear.
The ring-to-sun ratios are:
where:
gRSS is the ring-to-small sun gear ratio.
NR is the number of teeth in the ring gear.
NSS is the number of teeth in the small sun gear.
gRSS is the ring-to-large sun gear ratio.
NSL is the number of teeth in the large sun gear.
In terms of these gear ratios, the key kinematic constraints are:
The six degrees of freedom reduce to two independent degrees of freedom. The gear pairs are (1,2) = (LS,P), (SS,P), (P,R), and (P,P).
Warning
The gear ratio gRSS must be strictly greater than the gear ratio gRSL. The gear ratio gRSL must be strictly greater than one.
The torque transfers are:
where:
τSS is the torque transfer for the small sun gear.
τR is the torque transfer for the ring gear.
τloss(SS,R) is the torque transfer loss between the small sun gear and the ring gear.
τSL is the torque transfer for the large sun gear.
τloss(SL,R) is the torque transfer loss between the large sun gear and the ring gear.
In the ideal case where there is no torque loss, τloss = 0.
In the nonideal case, τloss ≠ 0. For more information, see Model Gears with Losses.
Assumptions and Limitations
The gears are assumed to be rigid.
Coulomb friction slows down simulation. For more information, see Adjust Model Fidelity.
Ports
Conserving
Parameters
More About
Extended Capabilities
Version History
Introduced in R2011a